137. GCD

Find the greatest common divisor (GCD) of n numbers.

Input. The first line contains the number of integers n (1 < n < 101). The second line contains n positive integers, each not exceeding 30000.

Output. Print one number – the GCD of the given numbers.

Sample input	Sample output
2 15 25	5

SOLUTION

GCD

Algorithm analysis

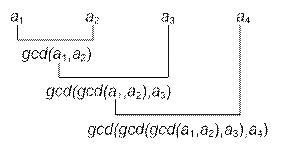
It is known that

GCD (a₁, a₂, …, a_i) = GCD (GCD (a₁, a₂, …, a_{i - 1}) , a_i)

Based on this, the greatest common divisor of two, three, ..., n numbers can be computed sequentially. For example, for four numbers, the following equality holds:

GCD (a₁, a₂, a₃, a₄) = GCD (GCD (GCD (GCD (0, a₁), a₂), a₃), a₄)

Algorithm implementation

The function gcd computes the greatest common divisor.

int gcd(int a, int b)

{

return (!b) ? a : gcd(b, a % b);

}

Read the input data and sequentially compute the GCD for the given n numbers, storing the result in the variable res.

res = 0;

scanf("%d", &n);

while (n--)

{

scanf("%d", &b);

res = gcd(res, b);

}

Print the answer.

printf("%d\n", res);

Python implementation

import math

Read the input data.

n = int(input())

lst = list(map(int,input().split()))

In the variable res, sequentially compute the GCD of the given n numbers.

res = 0

for x in lst:

res = math.gcd(res, x)

Print the answer.

print(res)